Un arreglo es un conjunto de celdas de memoria relacionadas entre si ya que todos tienen el mismo nombre y almacenan el mismo tipo de datos para referirse a una celda en particular algún elemento dentro del arreglo y entre corchetes [] el numero de posición del elemento dentro del arreglo.
El primer elemento se almacena en la posición 0 del arreglo, es decir el primer elemento del arreglo se conoce como a[0], el segundo como a[1], el séptimo como a[6] y en general el elemento de orden i del arreglo a se conoce como a[i-1].
El número de posición que aparece dentro de los corchetes se conoce como índice y debe ser un número entero o una expresión entera.
Ejemplo:
printf ("%i", a[0]+a[5]+a[10]);
x=a[7]/2;
x=a[4]=12;
Para declarar un arreglo se emplea la siguiente sintaxis: tipo_de_dato nombre_del_arreglo [número de elementos];
int a[12];
float f[10];
char nom_emp [30];
Ejemplo: #include <stdio.h>
#include <conio.h>
#define MAX 12
void main(){
int a[MAX], b[MAX], c[MAX], i, j=0, k=0;
clrscr();
printf ("Programa que almacena 12 numeros en un arreglo ");
printf ("y luego los separa en dos de acuerdo a su valor.\n");
for (i=0; i < MAX; i++){
printf ("Introduce el valor %i: ", i+1);
scanf ("%i", &a[i]);
}
for (i=0; i < MAX; i++)
if (a[i] < MAX){
b[j] = a[i];
j++;
}
else {
c[k] = a[i];
k++;
}
printf ("\nLos numeros quedan asi:\n\n");
for (i=0; i < j; i++)
printf ("%i\n", b[i]);
for (i=0; i < k; i++)
printf ("\t%i\n", c[i]);
getch();
}

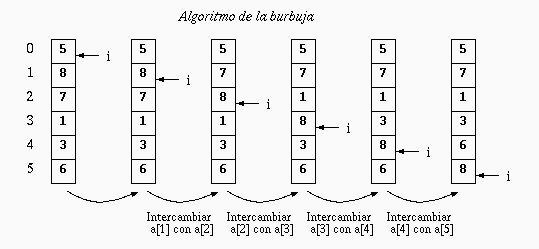
Algoritmo de ordenamiento Burbuja
Este algoritmo compara elementos consecutivos del arreglo uno con respecto del otro, si es mayor o menor según el tipo de ordenamiento y los cambia de posición. Este proceso se repite recorriendo todo el arreglo para posicionar un solo dato, por lo que es necesario repetirlo para los demás datos del arreglo. Su implementación es la siguiente:
#include <stdio.h>
#include <conio.h>
#include <stdlib.h>
#define TAM 10
void main(){
int a[TAM], temp, i, j;
clrscr();
randomize(); //Inicializa el generador de numeros aleatorios
printf ("Llenando arreglo con números aleatorios\n");
for (i=0; i< TAM; i++)
a[i]=random(100);
//Implementacion de Ordenamiento por burbuja de mayor a menor
for (j=1; j <= TAM; j++)
for (i=0; i< TAM-1; i++)
if (a[i] < a[i+1]){
temp = a[i];
a[i] = a[i+1];
a[i+1] = temp;
}
printf ("\nArreglo ordenado\n");
for (i=0; i< TAM; i++)
printf ("a[%d] = %d\n", i, a[i]);
getch();
}
Búsqueda Secuencial
Este algoritmo compara uno a uno los elementos del arreglo hasta recorrerlo por completo indicando si el número buscado existe. Su implementación es la siguiente:
#include <stdio.h>
#include <conio.h>
#include <stdlib.h>
#define TAM 10
void main(){
int a[TAM], temp, i, j, num;
clrscr();
randomize(); //Inicializa el generador de numeros aleatorios
printf ("Llenando arreglo con números aleatorios\n");
for (i=0; i< TAM; i++)
a[i]=random(100);
printf ("Numero a buscar? ");
scanf ("%d", &num);
for (i=0; i< TAM; i++)
if (a[i] == num){
printf ("\nValor encontrado");
printf ("\nPosicion: %d", i);
}
else
printf ("\nNo existe");
printf ("El arreglo era:\n");
for (i=0; i< TAM; i++)
printf ("%d ", a[i]);
getch();
}
Búsqueda Binaria
Este algoritmo permite buscar de una manera más eficiente un dato dentro de un arreglo, para hacer esto se determina el elemento central del arreglo y se compara con el valor que se esta buscando, si coincide termina la busqueda y en caso de no ser asi se determina si el dato es mayor o menor que el elemento central, de esta forma se elimina una mitad del arreglo junto con el elemento central para repetir el proceso hasta encontrarlo o tener solo un elemento en el arreglo. Para poder aplicar este algorimo se requiere que el arreglo este ordenado. Su implementación es la siguiente:
#include <stdio.h>
#include <conio.h>
#include <stdlib.h>
#define TAM 15
void main(){
int a[TAM], busca, temp, bajo, alto, central;
printf("Llenando el arreglo con números aleatorios\n");
randomize(); //Inicializa el generador de aleatorios
for (int i=0; i< TAM; i++)
a[i]=random(100);
//Implementacion de Ordenamiento por burbuja de menor a mayor
printf ("Ordenando arreglo...\n");
for (int j=1; j <= TAM; j++)
for (i=0; i< TAM-1; i++)
if (a[i] > a[i+1]){
temp = a[i];
a[i] = a[i+1];
a[i+1] = temp;
}
//Implementacion de busqueda binaria
printf ("\nIntroduce un numero a buscar: ");
scanf ("%d", &busca);
bajo = 0;
alto = TAM-1;
central = (bajo+alto)/2;
while (bajo < alto && busca != a[central]){
if(busca > a[central])
bajo = central+1;
else
alto = central-1;
central=(bajo+alto)/2;
}
if (busca == a[central])
printf("\n%d encontrado en posicion %d", busca, central);
else
printf("\n%d no existe", busca);
printf ("\n\nEl arreglo ordenado era\n\n");
for (i=0; i< TAM; i++)
printf ("%d ", a[i]);
getch();
}

Estructuras de datos
Las estructuras se definen como conjuntos de datos de diferente tipo. Se pueden declarar de las siguentes maneras:
struct nomina
{
char nom[80];
char puesto[40];
float sueldo;
int id;
}
struct nomina empleado_1, empleado_2, empleado[50];
struct
{
char nom[80];
char puesto[40];
float sueldo;
int id;
}
empleado_1, empleado_2, empleado[50];
typedef struct
{
char nom[80];
char puesto[40];
float sueldo:
int id;
} nomina;
nomina empleado_1; empleado_2; empleado[50];
Las estructuras, como cualquier otro tipo de dato, se pueden representar en arreglos. #include
struct
{
char nom[60];
char mat[40];
float cb, pc, cf;
flat prom;
} alumno[50];
float aux;
void main()
{
int i, n;
printf ("Cuantos alumnos? ");
scanf ("%d", &n);
flushall();
printf ("\nLectura de datos");
}
Arreglos multidimensionalesEs un tipo de dato estructurado, que está compuesto por dimensiones. Para hacer referencia a cada componente del arreglo es necesario utilizar n índices, uno para cada dimensión. El término dimensión representa el número de índices utilizados para referirse a un elemento particular en el arreglo. Los arreglos de más de una dimensión se llaman arreglos multidimensionales.Arreglos con múltiple subíndicesEs la representación de tablas de valores, consistiendo de información arreglada en renglones y columnas. Para identificar un elemento particular de la tabla, deberemos de especificar dos subíndices; el primero identifica el renglón del elemento y el segundo identifica la columna del elemento. A los arreglos que requieren dos subíndices para identificar un elemento en particular se conocen como arreglo de doble subíndice. Note que los arreglos de múltiples subíndices pueden tener más de dos subíndices. El estándar ANSI indica que un sistema ANSI C debe soportar por lo menos 12 subíndices de arreglo.Búsqueda por HashLa idea principal de este método consiste en aplicar una función que traduce el valor del elemento buscado en un rango de direcciones relativas. Una desventaja importante de este método es que puede ocasionar colisiones.Ejemplo :funcion hash (valor_buscado)iniciohash <- valor_buscado mod numero_primofininicio <- hash (valor)il <- inicioencontrado <- falsorepitesi arreglo[il] = valor entoncesencontrado <- verdaderoen caso contrarioil <- (il +1) mod Nhasta encontrado o il = inicioOrdenación por MezclaEste algoritmo consiste en partir el arreglo por la mitad, ordenar la mitad izquierda, ordenar la mitad derecha y mezclar las dos mitades ordenadas en un array ordenado. Este último paso consiste en ir comparando pares sucesivos de elementos (uno de cada mitad) y poniendo el valor más pequeño en el siguiente hueco.Ejemplo:procedimiento mezclar(dat,izqp,izqu,derp,deru)inicioizqa <- izqpdera <- derpind <- izqpmientras (izqa <= izqu) y (dera <= deru) hazsi arreglo[izqa] < dat[dera] entoncestemporal[ind] <- arreglo[izqa]izqa <- izqa + 1en caso contrariotemporal[ind] <- arreglo[dera]dera <- dera + 1ind <- ind +1mientras izqa <= izqu haztemporal[ind] <- arreglo[izqa]izqa <- izqa + 1ind <- ind +1mientras dera <= deru haztemporal[ind] <=dat[dera]dera <- dera + 1ind <- ind + 1para ind <- izqp hasta deru hazarreglo[ind] <- temporal[ind]fin
Quicksort
Quicksort es uno de los mejores algoritmos que existe para ordenar arreglos. La idea
general es la siguiente:
1. Si el número de elementos es 0 o 1, retornar.
2. Seleccionar un elemento del arreglo. Este elemento recibe el nombre de pivote.
3. Particionar los otros elementos en dos grupos disjuntos: A1 con los elementos menores
que el pivote y A2 con los elementos mayores o iguales que el pivote.
4. Retornar quicksort(A1), seguido del pivote y seguido de quicksort(A2).
Como puede verse, quicksort es un algoritmo recursivo y, por lo tanto, su análisis involucra la resolución de una relación de recurrencia.
Es evidente que siempre la selección del pivote es Q(1) y una vez seleccionado el pivote,
se realizan n 1 = Q(n) comparaciones para determinar los grupos A1 y A2.
Análisis de peor caso
El peor caso de quicksort es cuando el pivote siempre resulta ser el menor de los elementos del arreglo y por lo tanto el tiempo T(n) para ordenar los n elementos es la suma del
tiempo requerido para particionar que es Q(1) + Q(n) = Q(n) y la podemos aproximar
como kn (k > 0), el tiempo requerido para procesar un grupo de cero elementos que es
T(0) = Q(1) y el tiempo requerido para procesar n 1 elementos, que es T(n 1). Entonces nos queda, después de eliminar los términos absorbidos por la notación asintótica,
la expresión
T(n) = T(n 1) + kn (4)
que es una recurrencia lineal no homogénea.
El polinomio característico es x 1 = 0 y por lo tanto la única raíz es 1 y la solución
homogénea es c11
n = c1.
Para encontrar una solución particular podemos hacer T(n) = An2 + Bn + C y sustituyendo en 4 nos queda
An2 + Bn + C = A(n 1)
2 + B(n 1) + C + kn
= An2 2An + A + Bn B + C + kn
= An2 + n(B 2A + k) + (A B + C)
de donde nos queda A = k/2, B = k/2, C = 0.
La solución final es la suma de la solución homogénea y la solución particular y es
T(n) = k
2
n
2
k
2
n + c1 = Q(n
2
) (5)
Análisis de mejor caso
El mejor caso ocurre cuando el pivote siempre divide el arreglo en dos partes iguales. En
este caso T(n) sería el tiempo requerido para realizar la división del arreglo, que ya sabemos que es Q(n) y que aproximamos como kn (k > 0) y el tiempo requerido para ordenar
dos subarreglos cuyo tamaño no es superior a la mitad del arreglo original (de hecho los
tamaños son bn/2c y dn/2e 1). Entonces la relación de recurrencia la aproximamos
como
T(n) = 2T(n/2) + kn (6)
lo cual es ligeramente más que T(dn/2e 1) + T(bn/2c) + kn, pero es aceptable para
simplificar el análisis, ya que estamos interesados en una cota superior.
Para resolver esta ecuación de nuevo hacemos n = 2
m y nos queda T(2
m) = 2T(2
m1
) +
k2
m. Haciendo tm = T(2
m) y reordenando los términos nos queda
tm 2tm1 = k2
m (7)
y también, sustituyendo m por m 1
tm1 2tm2 = k2
m1
(8)
restando 7 menos 2 veces 8 nos queda tm 4tm1 + 4tm2 = 0, que es una relación de
recurrencia lineal homogénea cuyo polinomio característico es x
2 4x + 4 = (x 2)
2
,
que tiene la raíz doble 2. Entonces la solución de la recurrencia tm es
tm = c12
m + c2m2
m (9)
como n = 2
m entonces m = lg n y como tm = T(2
m) entonces
tlgn = T(2
lgn
) = T(n) = c12
lgn + c2 lg n2
lgn
= c1n + c2n lg n
= O(n lg n)
Análisis de caso promedio
En general, para ordenar n elementos, quicksort particiona (a un costo kn) el arreglo en
dos subarreglos de tamaño m y n m 1. Por lo tanto la relación de recurrencia general
es T(n) = T(m) + T(n m 1) + kn. Si asumimos que todas las posibles particiones son
igualmente probables, el tiempo promedio de T(m) y T(n m 1) es el mismo y es
En general, para ordenar n elementos, quicksort particiona (a un costo kn) el arreglo en
dos subarreglos de tamaño m y n m 1. Por lo tanto la relación de recurrencia general
es T(n) = T(m) + T(n m 1) + kn. Si asumimos que todas las posibles particiones son
igualmente probables, el tiempo promedio de T(m) y T(n m 1) es el mismo y es
1
n
n1
å
i=0
T(i) (10)
Entonces el tiempo promedio sería
T(n) = 2
n
n1
å
i=0
T(i) + kn (11)
multiplicando 11 por n tenemos
nT(n) = 2
n1
å
i=0
T(i) + kn2
(12)
sustituyendo n por n 1 nos queda
(n 1)T(n 1) = 2
n2
å
i=0
T(i) + k(n 1)
2
(13)
Si restamos 13 de 12 obtenemos
nT(n) (n 1)T(n 1) = 2T(n 1) + 2kn k (14)
Reagrupando nos queda
T(n) = (n + 1)
n
T(n 1) + 2k
k
n
(15)
Demostraremos por inducción que T(n) (n + 1)lg(n + 1) = O(n lg n), o lo que es lo
mismo, T(n 1) cn lg n. Fácilmente podemos encontrar valores de c y n suficientemente grandes tales que (n0 + 1)lg(n0 + 1) T(n0), así que lo que resta es demostrar
que T(n) c(n + 1)lg(n + 1) asumiendo que T(n 1) cn lg n.
Multipliquemos la hipótesis por n+1
n
y sumémosle 2k k
n
y nos queda
n + 1
n
T(n 1) + 2k
k
n
= T(n) c(n + 1)lg n + 2k
k
n
Entonces, sólo resta demostrar que
c(n + 1)lg n + 2k
k
n
c(n + 1)lg(n + 1)
lo cual es equivalente a
2k c(n + 1)lg(n + 1) c(n + 1)lg n +
k
n
= c(n + 1)lg (
n + 1
n
)
+
k
n
= cn lg (
1 +
1
n
)
+ c lg (
1 +
1
n
)
+
k
n
Cuando n es grande, los últimos dos términos tienden a cero, pero cn lg (
1 + 1
n
)
tiende a c
(calcular límite cuando n ! ¥ para verificar), la cual arbitrariamente podemos fijarla con
un valor mayor que 2k.
Mergesort
La operación clave del ordenamiento por fusión es la operación de fusión, la cual consiste
en combinar dos arreglos ordenados en un único arreglo ordenado más grande.
Si A es un arreglo y p, q,r son índices de A, tales que el subarreglo 1 está definido entre los
índices p y q y el subarreglo 2 está definido entre los índices q + 1 y r, entonces definimos
la operación de fusion como:
merge(A,p,q,r)
{
n1=q-p+1
n2=r-q
IZQ es un nuevo arreglo de tamaño n1+1
DER es un nuevo arreglo de tamaño n2+1
for (i=0;i<n1;i++) IZQ[i]=A[p+i];
for (j=0;j<n2;j++) DER[j]=A[q+1+j];
IZQ[n1]=INFINITO;
DER[n2]=INFINITO;
i=1;
j=1;
for (k=p;k<=r;k++)
if (IZQ[i]<=DER[j])
A[k] = IZQ[i++];
else
A[k] = DER[j++];
}
Si n = r p, entonces el tiempo de ejecución es Q(n). El centinela sería la evaluación de
la condición en el ciclo (k<=r), que se ejecuta n + 1 = Q(n) veces.
El procedimiento de ordenamiento por fusión es entonces:
mergesort(A,p,r)
{
if (p<r) {
q=(p+r)/2;
mergesort(A,p,q);
mergesort(A,q+1,r);
merge(A,p,q,r);
}
}
El tiempo de ejecución es T(n) = 2T(n/2) + kn, donde el T(n/2) es el tiempo que toma
ordenar un subarreglo de la mitad del tamaño y kn = Q(n) es el tiempo que toma realizar
la fusión de los dos subarreglos. Esta relación de recurrencia es idéntica a la correspondiente al mejor caso de quicksort y sabemos que el resultado es Q(n log(n)).
Arreglos de tamaño variable (listas basadas en arreglos)
Con frecuencia, se desea tener una lista relativamente pequeña de elementos, pero de
tamaño variable y en muchos casos los arreglos son la opción más apropiada. Para minimizar el costo de la asignación de memoria, el arreglo debe crecer en pedazos más o menos
grandes y toda la información sobre el arreglo se debe manetener organizada en un solo
lugar.
Los arreglos son la manera más simple de agrupar datos.
Proporcionan las siguientes operaciones en tiempo O(1): agregar al final del arreglo, borrar al final del arreglo y obtener el i-ésimo elemento.
Las siguientes operaciones tienen un tiempo O(n): añadir en posición i, encontrar elemento e, borrar posición i, borrar elemento e.
Vídeos :
http://www.youtube.com/watch?v=mEvjuG_tbqY




No hay comentarios:
Publicar un comentario